Diferencia entre revisiones de «Final del 01/08/18 (Algoritmos III)»
(→a) |
|||
| (No se muestran 7 ediciones intermedias de 4 usuarios) | |||
| Línea 23: | Línea 23: | ||
== Ejercicio 4 == | == Ejercicio 4 == | ||
Un grafo G es coloreable en forma única si todo coloreo con <math>\chi(G)</math> colores induce la misma partición de los vértices. | Un grafo G es coloreable en forma única si todo coloreo con <math>\chi(G)</math> colores induce la misma partición de los vértices. Mostrar que si G es coloreable en forma única, el subgrafo inducido por dos conjuntos cualesquiera de la partición inducida por los <math>\chi(G)</math>-colores es un subgrafo conexo. | ||
== Ejercicio 5 == | == Ejercicio 5 == | ||
| Línea 58: | Línea 58: | ||
Tomar dos conjuntos <math>A</math> y <math>B</math> de la partición inducida <math>P</math>. | Tomar dos conjuntos <math>A</math> y <math>B</math> de la partición inducida <math>P</math>. | ||
Suponer que no son conexos. | Suponer que no son conexos. Entonces ... | ||
=== espero que bien === | |||
Al no ser conexos, en el subgrafo inducido de <math>A</math> y <math>B</math> existen dos componentes conexas (como mínimo). | |||
Llamemoslas <math>C_1</math> <math>C_2</math>, además algunos vértices de <math>C_1</math> caen en A y otros en B, y lo mismo con <math>C_2</math>. | |||
Entonces podemos elegir todos los nodos de <math>V(C_1) \cap A</math> y swapear sus colores con <math>V(C_2) \cap B</math>. | |||
Con lo cual, tenemos una coloración de mismo número cromático, que induce otra partición de los vértices. | |||
Un dibujo puede ayudar a visualizar: | |||
------- | |||
A: -/ \- B: | |||
/ \ ------- | |||
/ a(q)----\------/---d(p)\- | |||
/ \ / | \ | |||
| | / | \ | |||
| b(q)-----+--+------+ | | |||
| | \ / | |||
\ / \ / | |||
\ c(q)--------------e(p)/- | |||
\ / ------- | |||
-\ /- | |||
------- | |||
A: tiene 3 vértices, a, b, c con color q y B tiene 2 (d, e) con color p. | |||
Si cambiamos c(q) y e(p) por c(p) y e(q), movimos el vértice c al conjunto B y el e al A. | |||
Con esto demostramos la contra recíproca: si el subgrafo inducido por dos conjuntos cualesquiera de la partición inducida por los <math>\chi(G)</math>-colores *no* es un subgrafo conexo; entonces el grafo original no es coloreable de forma única. | |||
=== mal resuelto === | |||
(Como dice el título... esto está *mal* resuelto. Que no sean conexos *no* significa que no tengan aristas entre si y que por lo tanto se pueda usar el mismo color. | |||
Lo dejo por si alguien pensándolo comete la misma metida de pata.) | |||
Pero entonces se les puede asignar el mismo color pues entre ellos no hay adyacencias en el grafo original y con el resto de los vértices no hay problemas pues pertenecen a otro conjunto, es decir tenían otro color. | Pero entonces se les puede asignar el mismo color pues entre ellos no hay adyacencias en el grafo original y con el resto de los vértices no hay problemas pues pertenecen a otro conjunto, es decir tenían otro color. | ||
| Línea 78: | Línea 116: | ||
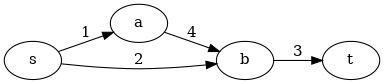
[[Archivo:A.png]] | [[Archivo:A.png]] | ||
<math>S={s}, S'={s, a, b}</math> | <math>S=\{s\}, S'=\{s, a, b\}</math> | ||
<math>c(S) = 3, c(S') = 1+2 = 3</math> | <math>c(S) = 3, c(S') = 1+2 = 3</math> | ||
todas las aristas tienen distintas capacidades y sin embargo hay más de un corte mínimo. | todas las aristas tienen distintas capacidades y sin embargo hay más de un corte mínimo. | ||
=== b,c === | |||
usando la definición, un corte mínimo S es aquel tal que <math>c(S) \leq c(S')</math> con <math>S'</math> cualquier otro corte mínimo. | |||
Entonces se puede escribir esta condición: | |||
<math> \sum\limits_{e \in SS_c} c(e) \leq \sum\limits_{e' \in S'S_c'} c(e') </math> | |||
con <math>S_c = V\backslash S</math> es decir, el complemento. | |||
si multiplicamos por una constante mayor que cero, no cambia nada: | |||
<math> \sum\limits_{e \in SS_c} \lambda c(e) \leq \sum\limits_{e' \in S'S_c'} \lambda c(e') </math> | |||
por distributiva: | |||
<math> \lambda \sum\limits_{e \in SS_c} c(e) \leq \lambda \sum\limits_{e' \in S'S_c'} c(e') </math> | |||
por ser != 0 | |||
<math> \sum\limits_{e \in SS_c} c(e) \leq \sum\limits_{e' \in S'S_c'} c(e') </math> | |||
Si bien, la desigualdad no cambia, el valor de cada corte mínimo, si. | |||
=== d, e === | |||
Planteamos lo mismo que en b pero esta vez ... | |||
<math> \sum\limits_{e \in SS_c} c(e) + \lambda \leq \sum\limits_{e' \in S'S_c'} c(e') + \lambda </math> | |||
<math> \sum\limits_{e \in SS_c} c(e) + \sum\limits_{e \in SS_c} \lambda \leq \sum\limits_{e' \in S'S_c'} c(e') + \sum\limits_{e' \in S'S_c'} \lambda </math> | |||
es decir, se suman las constantes, tantas veces como aristas hay en los conjuntos <math>SS_c \text{y} S'S_c'</math> respectivamente. | |||
entonces podemos re escribir: | |||
<math> \sum\limits_{e \in SS_c} c(e) - \sum\limits_{e' \in S'S_c'} c(e') \leq |S'S_c'|\lambda - |SS_c|\lambda </math> | |||
si llamamos dc a la diferencias de las capacidades, a la parte izquierda de la inecuación: | |||
<math> \frac{\text{dc}}{\lambda} \leq |S'S_c'| - |SS_c| </math> | |||
Tenemos una condición para saber cuando un corte puede dejar de ser mínimo al sumar las capacidades por una constante mayor a 0. | |||
<math> \frac{\text{dc}}{\lambda} > |S'S_c'| - |SS_c| </math> | |||
es decir, si encontramos una constante que no compence la diferencia en capacidades vs la diferencia de aristas para un corte mínimo y algún otro corte cualquiera, vamos a tener un cambio en el orden y por lo tanto al menos <math>S</math> dejará de ser un corte mínimo. | |||
Revisión actual - 05:32 22 oct 2018
Final escrito de Paula Zabala. Eramos tres. Así que tampoco se confíen con que n grande escrito. A lo sumo será: n grande escrito.
Enunciados
Ejercicio 1
a) Nombrar las técnicas algorítmicas vistas en la materia.
b) Describir alguna de ellas
Ejercicio 2
Modificaciones del algoritmo de Dijkstra:
a) para contar el número de caminos mínimos de v a w
b) para que de todos los caminos mínimos, se elija el de menor número de aristas.
Ejercicio 3
Dado un grafo G=(V,X) con una función de costo definida sobre sus airstas, . Probar que si tal que , entonces pertenece a todo árbol generador mínimo de G
Ejercicio 4
Un grafo G es coloreable en forma única si todo coloreo con colores induce la misma partición de los vértices. Mostrar que si G es coloreable en forma única, el subgrafo inducido por dos conjuntos cualesquiera de la partición inducida por los -colores es un subgrafo conexo.
Ejercicio 5
Decidir si las siguientes afirmaciones son verdaderas o falsas. Justificar.
- a) Si todos los arcos de una rede tienen diferentes capacidades, la red tiene un único corte mínimo.
- b) Si se multiplican las capacidades de todos los arcos por , el o los cortes mínimos no cambian.
- c) Si se multiplican las capacidades de todos los arcos por , el valor del o de los cortes mínimos no cambia
- d) Si se suma a las capacidades de todos los arcos , el o los cortes mínimos no cambia.
- e) Si se suma a las capacidades de todos los arcos , el valor del o de los cortes mínimo no cambia.
Ejercicio 6
- a) ¿cuando un problema pertenece a la clase P?
- b) ¿cuando un problema pertenece a la clase NP?
- c) ¿cuando un problema pertenece a la clase NP-C?
- d) ¿Qué es una reducción polinomial de un problema de decisión a uno ?
- e) Demostrar que el problema de conjunto independiente máximo (versión desición) pertenece a la clase NP.
- f) En la práctica, ¿cómo se demuestra que un problema pertenece a la clase NP-C? Justificar.
- g) Enunciar 5 problemas estudiados en la materia que sean P y 5 que sean NP-C.
Soluciones
Ejercicio 3
idea
Hacer un absurdo, suponer que existe un T Arbol Generador Mínimo que no contiene esa arista y luego mostrar que existe un árbol menor que la arista.
Ejercicio 4
Absurdo de nuevo.
Tomar dos conjuntos y de la partición inducida .
Suponer que no son conexos. Entonces ...
espero que bien
Al no ser conexos, en el subgrafo inducido de y existen dos componentes conexas (como mínimo).
Llamemoslas , además algunos vértices de caen en A y otros en B, y lo mismo con .
Entonces podemos elegir todos los nodos de y swapear sus colores con .
Con lo cual, tenemos una coloración de mismo número cromático, que induce otra partición de los vértices.
Un dibujo puede ayudar a visualizar:
-------
A: -/ \- B:
/ \ -------
/ a(q)----\------/---d(p)\-
/ \ / | \
| | / | \
| b(q)-----+--+------+ |
| | \ /
\ / \ /
\ c(q)--------------e(p)/-
\ / -------
-\ /-
-------
A: tiene 3 vértices, a, b, c con color q y B tiene 2 (d, e) con color p.
Si cambiamos c(q) y e(p) por c(p) y e(q), movimos el vértice c al conjunto B y el e al A.
Con esto demostramos la contra recíproca: si el subgrafo inducido por dos conjuntos cualesquiera de la partición inducida por los -colores *no* es un subgrafo conexo; entonces el grafo original no es coloreable de forma única.
mal resuelto
(Como dice el título... esto está *mal* resuelto. Que no sean conexos *no* significa que no tengan aristas entre si y que por lo tanto se pueda usar el mismo color. Lo dejo por si alguien pensándolo comete la misma metida de pata.)
Pero entonces se les puede asignar el mismo color pues entre ellos no hay adyacencias en el grafo original y con el resto de los vértices no hay problemas pues pertenecen a otro conjunto, es decir tenían otro color.
Entonces existe un coloreo que induce una partición tal que pero , absurdo, la partición era única.
El absurdo provino de suponer que *no* son conexos ergo deben serlo.
Ejercicio 5
a) F b) V c) F d) F e) F
a
todas las aristas tienen distintas capacidades y sin embargo hay más de un corte mínimo.
b,c
usando la definición, un corte mínimo S es aquel tal que con cualquier otro corte mínimo.
Entonces se puede escribir esta condición:
con es decir, el complemento.
si multiplicamos por una constante mayor que cero, no cambia nada:
por distributiva:
por ser != 0
Si bien, la desigualdad no cambia, el valor de cada corte mínimo, si.
d, e
Planteamos lo mismo que en b pero esta vez ...
es decir, se suman las constantes, tantas veces como aristas hay en los conjuntos respectivamente.
entonces podemos re escribir:
si llamamos dc a la diferencias de las capacidades, a la parte izquierda de la inecuación:
Tenemos una condición para saber cuando un corte puede dejar de ser mínimo al sumar las capacidades por una constante mayor a 0.
es decir, si encontramos una constante que no compence la diferencia en capacidades vs la diferencia de aristas para un corte mínimo y algún otro corte cualquiera, vamos a tener un cambio en el orden y por lo tanto al menos dejará de ser un corte mínimo.