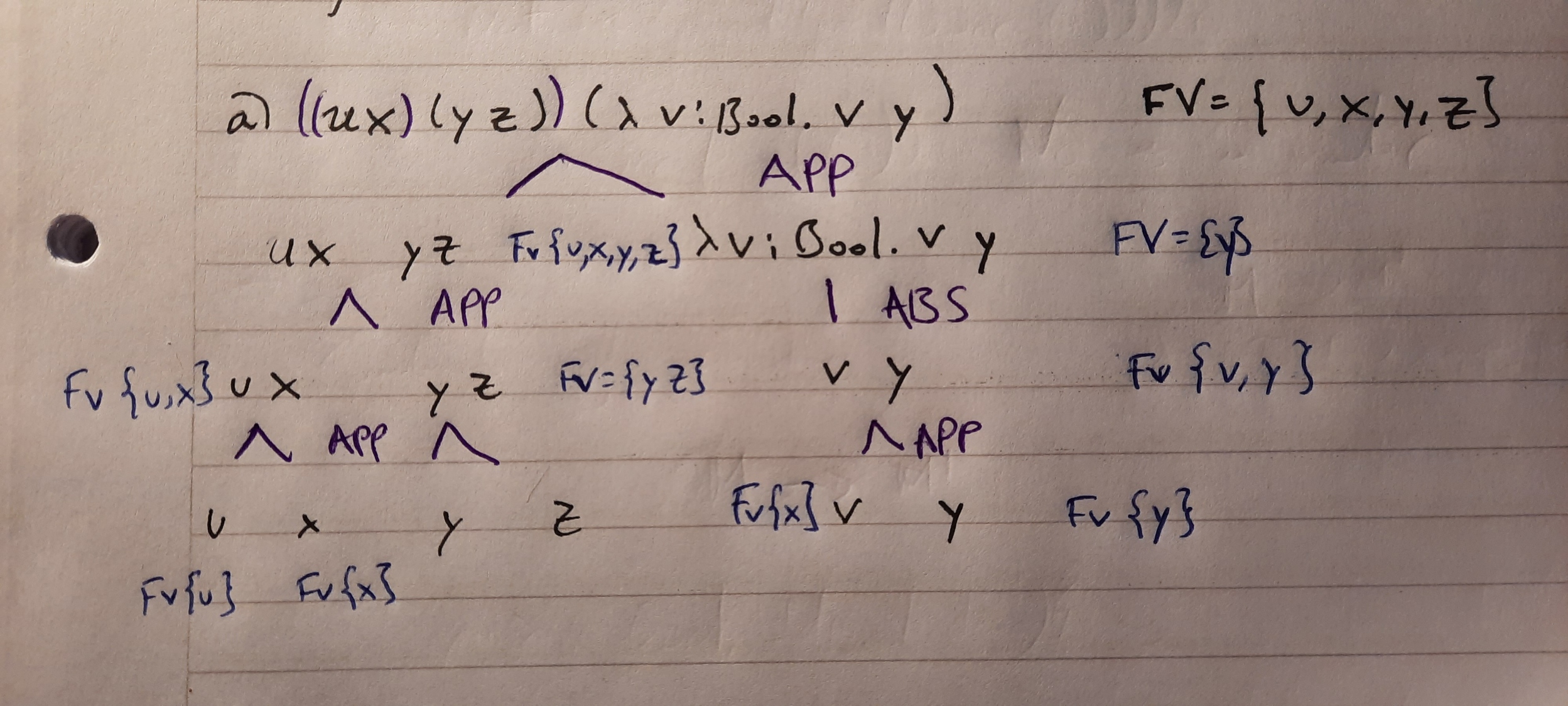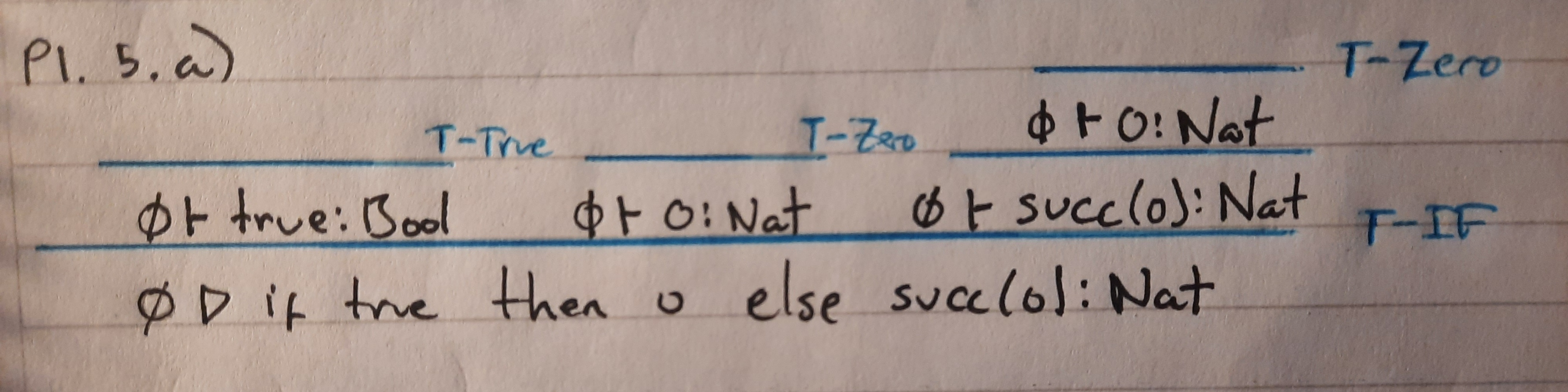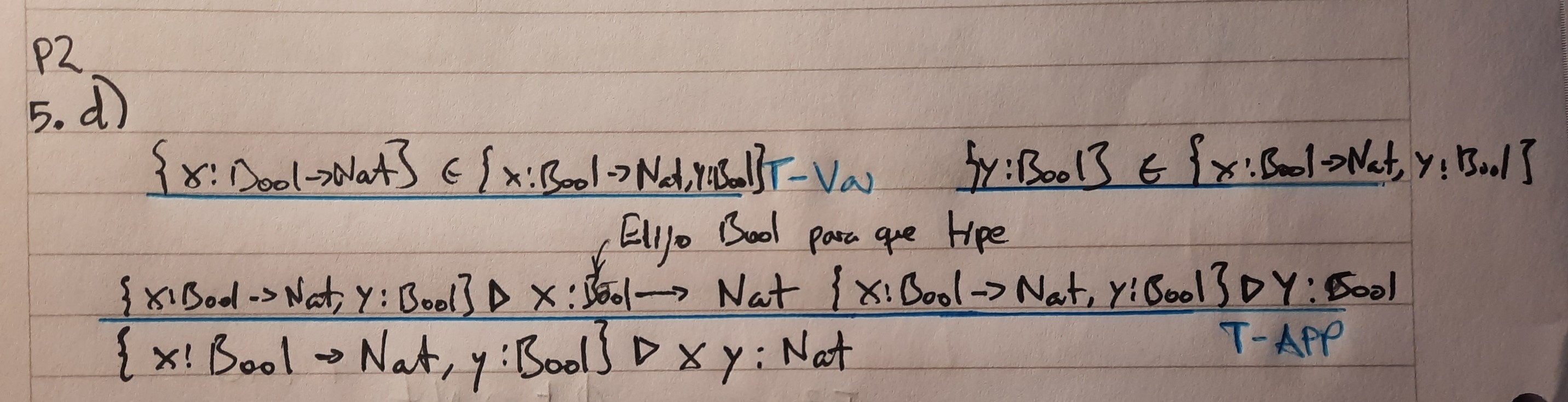Diferencia entre revisiones de «Práctica 2 (Paradigmas)»
Sin resumen de edición |
|||
| (No se muestran 19 ediciones intermedias de 3 usuarios) | |||
| Línea 70: | Línea 70: | ||
== Ejercicio 4 == | == Ejercicio 4 == | ||
Para los siguientes términos: | Para los siguientes términos: | ||
a) u x (y z) (λv : Bool. v y) | a) u x (y z) (λv : Bool. v y) | ||
( (u x) (y z) ) (λv : Bool. v y ) | |||
b) (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v w | b) (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v w | ||
( ( ( λx: (Bool -> Nat) -> Bool. λy: Bool ->Nat. λz : Bool. (x z) (y z) ) u) v ) w | |||
c) w (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v | c) w (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v | ||
( ( w (λx : (Bool -> Nat) -> Bool. λy Bool -> Nat. λz: Bool. (x z) (y z) ) ) u) v | |||
Se pide: | Se pide: | ||
i Insertar todos los paréntesis de acuerdo a la convención usual. | i Insertar todos los paréntesis de acuerdo a la convención usual. | ||
[[Archivo:PLPej4a.jpg|left]] | |||
[[Archivo:Ej4b.jpg|none]] | |||
c. Muy parecido al b pero queda una abstracción a la derecha. | |||
ii Dibujar el árbol sintáctico de cada una de las expresiones. | ii Dibujar el árbol sintáctico de cada una de las expresiones. | ||
iii Indicar en el árbol cuáles ocurrencias de variables aparecen ligadas y cuáles libres. | iii Indicar en el árbol cuáles ocurrencias de variables aparecen ligadas y cuáles libres. | ||
| Línea 87: | Línea 101: | ||
(λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u | (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u | ||
En el b | |||
TIPADO | |||
== Ejercicio 5 (Derivaciones) == | |||
Demostrar o explicar por qué no puede demostrarse cada uno de los siguientes juicios de tipado. | |||
a) ∅ . if true then 0 else succ(0) : Nat | |||
[[Archivo:5.a.jpg|none]] | |||
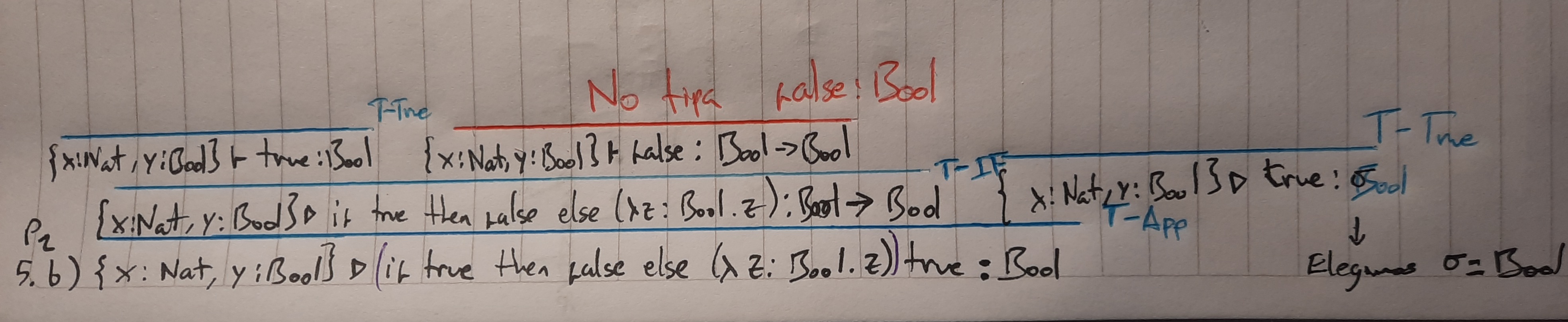
b) {x : Nat, y : Bool} . if true then false else (λz : Bool. z) true : Bool | |||
[[Archivo:5b.jpg|none]] | |||
c) ∅ . if λx: Bool. x then 0 else succ(0) : Nat | |||
Falta el resto del cuerpo del if ya que se agrupa de izq pero el lambda se come toda la expresión si no se le ponen parentesis. | |||
d) {x : Bool → Nat, y : Bool} . x y : Nat | |||
[[Archivo:5d.jpg|none]] | |||
== Ejercicio 6 == | |||
Determinar qué tipo representa σ en cada uno de los siguientes juicios de tipado. | |||
a) ∅ . succ(0) : σ NAT | |||
b) ∅ . isZero(succ(0)) : σ BOOL | |||
c) ∅ . if (if true then false else false) then 0 else succ(0) : σ NAT | |||
== Ejercicio 7 == | |||
Determinar qué tipos representan σ y τ en cada uno de los siguientes juicios de tipado. Si hay más de una | |||
solución, o si no hay ninguna, indicarlo. | |||
a) {x: σ} . isZero(succ(x)) : τ ----- σ = Nat y τ = Bool | |||
b) ∅ . (λx: σ. x)(λy : Bool. 0) : σ ----- σ = Bool -> Nat | |||
c) {y : τ} . if (λx: σ. x) then y else succ(0) : σ ----- No tiene solución | |||
d) {x: σ} . x y : τ ----- σ = No tiene solución | |||
e) {x: σ, y : τ} . x y : τ ----- σ = CualquierCosa -> τ y τ=CualquierCosa | |||
f) {x: σ} . x true : τ ------σ = Bool -> τ y τ=CualquierCosa | |||
g) {x: σ} . x true : σ ----- σ = Bool -> CualquierCosa | |||
h) {x: σ} . x x : τ ------ No tiene solución | |||
== Ejercicio 8 == | |||
Mostrar un término que no sea tipable y que no tenga variables libres ni abstracciones. | |||
isZero(True) | |||
== Ejercicio 9 == | |||
Mostrar un juicio de tipado que sea demostrable en el sistema actual pero que no lo sea al cambiar (T-ABS) | |||
por la siguiente regla. Mostrar la demostración del juicio original. | |||
Γ . M : τ | |||
T-ABS2 | |||
Γ . λx: σ. M : σ → τ | |||
Para esta nueva regla no tipa ∅ . (λx: Bool. x):Bool -> Bool porque no se agrega x: Bool al contexto. | |||
SEMÁNTICA | |||
== Ejercicio 10 == | |||
Sean σ, τ, ρ tipos. Según la de�nición de sustitución, calcular: | |||
a) (λy : σ. x (λx: τ. x)){x ← (λy : ρ. x y)} | |||
b) (y (λv : σ. x v)){x ← (λy : τ. v y)} | |||
Renombrar variables en ambos términos para no cambiar el signi�cado del término. | |||
[[Archivo:PLP-PRACTICA2.10.jpg|none]] | |||
== Ejercicio 11 (Valores) == | |||
Dado el conjunto de valores visto en clase: | |||
V := λx: σ. M | true | false | 0 | succ(V ) | |||
Determinar si cada una de las siguientes expresiones es o no un valor: | |||
a) (λx: Bool. x) true -------- Es un valor | |||
b) λx: Bool. 2 -------- Es un valor | |||
c) λx: Bool. pred(2) -------- Es un valor | |||
d) λy : Nat. (λx: Bool. pred(2)) true -------- Es un valor | |||
e) x -------- No es un valor | |||
f) succ(succ(0)) -------- Es un valor | |||
== Ejercicio 12 (Programa, Forma Normal) == | |||
Para el siguiente ejercicio, considerar el cálculo sin la regla pred(0) → 0 | |||
Un programa es un término que tipa en el contexto vacío (es decir, no puede contener variables libres). | |||
Para cada una de las siguientes expresiones | |||
a) Determinar si puede ser considerada un programa. | |||
b) Si vale (a), ¾Cuál es el resultado de su evaluación? Determinar si se trata de una forma normal, y en caso | |||
de serlo, si es un valor o un error. | |||
i (λx: Bool. x) true -- Es un programa, da true | |||
ii λx: Nat. pred(succ(x)) -- Es un programa, da la identidad | |||
iii λx: Nat. pred(succ(y)) -- No es un programa, tiene variables libres | |||
iv (λx: Bool. pred(isZero(x))) true -- Es un programa, da error | |||
v (λf : Nat → Bool. f 0) (λx: Nat. isZero(x)) -- Es un programa, da true | |||
vi (λf : Nat → Bool. x) (λx: Nat. isZero(x)) -- No es un programa, tiene variables libres | |||
vii (λf : Nat → Bool. f pred(0)) (λx: Nat. isZero(x)) -- Es un programa, da error porque se saco pred(0) | |||
viii fix (λy : Nat. succ(y)) -- Es un programa, da error porque no termina | |||
== Ejercicio 13 (Determinismo) == | |||
a) Es cierto que la relación definida → es determinística (o una función parcial)? Más precisamente, pasa que si M → N y M → N` | |||
entonces N = N` ? -- SI | |||
b) Vale lo mismo con muchos pasos? Es decir, ¾es cierto que si M →→ M` y M →→ M`` entonces M` = M``? -- SI | |||
c) Acaso es cierto que si M → M` y M →→ M`` entonces M` = M``? -- NO | |||
== Ejercicio 14 == | |||
a) Da lo mismo evaluar succ(pred(M)) que pred(succ(M))? ¾Por qué? -- No, porque pred(succ(0)) = 0 pero succ(pred(0)) = 1 | |||
b) Es verdad que para todo M vale que isZero(succ(M)) →→ false? Si no lo es, ¾para qué términos vale? -- Vale para todo M nat | |||
c) Para qué términos M vale que isZero(pred(M)) →→ true? (Hay infinitos). -- Pueden ser combinaciones de pred^n(succ^n(0)) para un n entero. | |||
Revisión actual - 03:42 7 oct 2021
SINTAXIS
Ejercicio 1
Determinar qué expresiones son sintácticamente válidas (es decir, pueden ser generadas con las gramáticas presentadas) y determinar a qué categoría pertenecen (expresiones de términos o expresiones de tipos):
a) x ---------VALIDO, expresiones de términos
b) x x ---------VALIDO, expresiones de términos
c) M --------- No es un término
d) M M --------- No es un término
e) true false ---------VALIDO, expresiones de términos
f) true succ(false true) ---------VALIDO, expresiones de términos
g) λx.isZero(x) --------- Falta tipo
h) λx: σ. succ(x) --------- Falta tipo, sigma no es un tipo valido
i) λx: Bool. succ(x) ---------VALIDO, expresiones de términos
j) λx: if true then Bool else Nat. x --------- Falta tipo
k) σ --------- Sigma no es un tipo valido
l) Bool ---------VALIDO, expresiones de tipos
m) Bool → Bool ---------VALIDO, expresiones de tipos
n) Bool → Bool → Nat ---------VALIDO, expresiones de tipos
ñ) (Bool → Bool) → Nat ---------VALIDO, expresiones de tipos
o) succ true --------- Si succ fuera una variables seria una aplicación, pero el enunciado dice que las variables se representan con una letra por lo cual a succ como termino le faltan los paréntesis.
p) λx: Bool. if 0 then true else 0 succ(true) ---------VALIDO, expresiones de términos
Ejercicio 2
Mostrar un término que utilice al menos una vez todas las reglas de generación de la gramática y exhibir su árbol sintáctico.
(λx: Bool. if isZero(succ(pred(x))) then true else false) x
app / \
(λx: Bool. if isZero(succ(pred(x))) then true else false) x
abs /
if isZero(succ(pred(x))) then true else false
ITF / | \
isZero(succ(pred(x)) true false
/
succ(pred(x))
/
pred(x)
/
x
Ejercicio 3
a) Marcar las ocurrencias del término x como subtérmino en λx: Nat. succ((λx: Nat. x) x).
Dos ocurrencias, en el lamda, y en la aplicación dentro den succ()
b) Ocurre x1 como subtérmino en λx1 : Nat. succ(x2)?
No, x1 es una variable ligada y no un subtermino.
c) Ocurre x (y z) como subtérmino en u x (y z)?
u x (y z) = ((u x) (y z) ) se agrupa a izq, por lo tanto no es subtermino en el árbol sintáctico.
Ejercicio 4
Para los siguientes términos:
a) u x (y z) (λv : Bool. v y)
( (u x) (y z) ) (λv : Bool. v y )
b) (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v w
( ( ( λx: (Bool -> Nat) -> Bool. λy: Bool ->Nat. λz : Bool. (x z) (y z) ) u) v ) w
c) w (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v
( ( w (λx : (Bool -> Nat) -> Bool. λy Bool -> Nat. λz: Bool. (x z) (y z) ) ) u) v
Se pide:
i Insertar todos los paréntesis de acuerdo a la convención usual.
c. Muy parecido al b pero queda una abstracción a la derecha.
ii Dibujar el árbol sintáctico de cada una de las expresiones.
iii Indicar en el árbol cuáles ocurrencias de variables aparecen ligadas y cuáles libres.
iv ¾En cuál de los términos anteriores ocurre la siguiente expresión como subtérmino?
(λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u
En el b
TIPADO
Ejercicio 5 (Derivaciones)
Demostrar o explicar por qué no puede demostrarse cada uno de los siguientes juicios de tipado.
a) ∅ . if true then 0 else succ(0) : Nat
b) {x : Nat, y : Bool} . if true then false else (λz : Bool. z) true : Bool
c) ∅ . if λx: Bool. x then 0 else succ(0) : Nat
Falta el resto del cuerpo del if ya que se agrupa de izq pero el lambda se come toda la expresión si no se le ponen parentesis.
d) {x : Bool → Nat, y : Bool} . x y : Nat
Ejercicio 6
Determinar qué tipo representa σ en cada uno de los siguientes juicios de tipado.
a) ∅ . succ(0) : σ NAT
b) ∅ . isZero(succ(0)) : σ BOOL
c) ∅ . if (if true then false else false) then 0 else succ(0) : σ NAT
Ejercicio 7
Determinar qué tipos representan σ y τ en cada uno de los siguientes juicios de tipado. Si hay más de una solución, o si no hay ninguna, indicarlo.
a) {x: σ} . isZero(succ(x)) : τ ----- σ = Nat y τ = Bool
b) ∅ . (λx: σ. x)(λy : Bool. 0) : σ ----- σ = Bool -> Nat
c) {y : τ} . if (λx: σ. x) then y else succ(0) : σ ----- No tiene solución
d) {x: σ} . x y : τ ----- σ = No tiene solución
e) {x: σ, y : τ} . x y : τ ----- σ = CualquierCosa -> τ y τ=CualquierCosa
f) {x: σ} . x true : τ ------σ = Bool -> τ y τ=CualquierCosa
g) {x: σ} . x true : σ ----- σ = Bool -> CualquierCosa
h) {x: σ} . x x : τ ------ No tiene solución
Ejercicio 8
Mostrar un término que no sea tipable y que no tenga variables libres ni abstracciones.
isZero(True)
Ejercicio 9
Mostrar un juicio de tipado que sea demostrable en el sistema actual pero que no lo sea al cambiar (T-ABS) por la siguiente regla. Mostrar la demostración del juicio original.
Γ . M : τ T-ABS2 Γ . λx: σ. M : σ → τ
Para esta nueva regla no tipa ∅ . (λx: Bool. x):Bool -> Bool porque no se agrega x: Bool al contexto.
SEMÁNTICA
Ejercicio 10
Sean σ, τ, ρ tipos. Según la de�nición de sustitución, calcular:
a) (λy : σ. x (λx: τ. x)){x ← (λy : ρ. x y)}
b) (y (λv : σ. x v)){x ← (λy : τ. v y)}
Renombrar variables en ambos términos para no cambiar el signi�cado del término.
Ejercicio 11 (Valores)
Dado el conjunto de valores visto en clase:
V := λx: σ. M | true | false | 0 | succ(V )
Determinar si cada una de las siguientes expresiones es o no un valor:
a) (λx: Bool. x) true -------- Es un valor
b) λx: Bool. 2 -------- Es un valor
c) λx: Bool. pred(2) -------- Es un valor
d) λy : Nat. (λx: Bool. pred(2)) true -------- Es un valor
e) x -------- No es un valor
f) succ(succ(0)) -------- Es un valor
Ejercicio 12 (Programa, Forma Normal)
Para el siguiente ejercicio, considerar el cálculo sin la regla pred(0) → 0
Un programa es un término que tipa en el contexto vacío (es decir, no puede contener variables libres).
Para cada una de las siguientes expresiones
a) Determinar si puede ser considerada un programa.
b) Si vale (a), ¾Cuál es el resultado de su evaluación? Determinar si se trata de una forma normal, y en caso de serlo, si es un valor o un error.
i (λx: Bool. x) true -- Es un programa, da true ii λx: Nat. pred(succ(x)) -- Es un programa, da la identidad iii λx: Nat. pred(succ(y)) -- No es un programa, tiene variables libres iv (λx: Bool. pred(isZero(x))) true -- Es un programa, da error v (λf : Nat → Bool. f 0) (λx: Nat. isZero(x)) -- Es un programa, da true vi (λf : Nat → Bool. x) (λx: Nat. isZero(x)) -- No es un programa, tiene variables libres vii (λf : Nat → Bool. f pred(0)) (λx: Nat. isZero(x)) -- Es un programa, da error porque se saco pred(0) viii fix (λy : Nat. succ(y)) -- Es un programa, da error porque no termina
Ejercicio 13 (Determinismo)
a) Es cierto que la relación definida → es determinística (o una función parcial)? Más precisamente, pasa que si M → N y M → N` entonces N = N` ? -- SI
b) Vale lo mismo con muchos pasos? Es decir, ¾es cierto que si M →→ M` y M →→ M`` entonces M` = M``? -- SI
c) Acaso es cierto que si M → M` y M →→ M`` entonces M` = M``? -- NO
Ejercicio 14
a) Da lo mismo evaluar succ(pred(M)) que pred(succ(M))? ¾Por qué? -- No, porque pred(succ(0)) = 0 pero succ(pred(0)) = 1
b) Es verdad que para todo M vale que isZero(succ(M)) →→ false? Si no lo es, ¾para qué términos vale? -- Vale para todo M nat
c) Para qué términos M vale que isZero(pred(M)) →→ true? (Hay infinitos). -- Pueden ser combinaciones de pred^n(succ^n(0)) para un n entero.