Diferencia entre revisiones de «Recuperatorio Segundo Parcial 1C/2015 (Algoritmos II)»
(Transcribo ejercicio 3 sin imagen de ejemplo) |
(Agrega la imagen de ejemplo al ejercicio 3) |
||
| Línea 70: | Línea 70: | ||
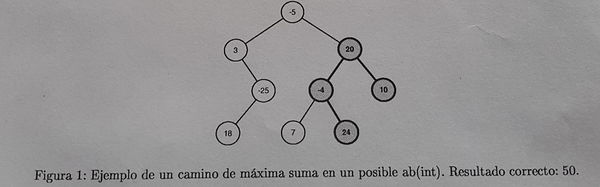
Dado un árbol binario de números enteros, se desea calcular la máxima suma de los nodos pertenecientes a un camino entre dos nodos cualesquiera del árbol. Un camino entre dos nodos <math>n_1</math> y <math>n_2</math> está formado por todos los nodos que hay que atravesar en el árbol para llegar desde <math>n_1</math> hasta <math>n_2</math>, incluyéndolos a ambos. Un camino entre un nodo y sí mismo está formado únicamente por ese nodo. El algoritmo debe recorrer <b>como máximo una vez</b> cada nodo del árbol, que no necesariamente es completo. Se considerará incorrecto a un algoritmo que no cumpla con esta condición. | Dado un árbol binario de números enteros, se desea calcular la máxima suma de los nodos pertenecientes a un camino entre dos nodos cualesquiera del árbol. Un camino entre dos nodos <math>n_1</math> y <math>n_2</math> está formado por todos los nodos que hay que atravesar en el árbol para llegar desde <math>n_1</math> hasta <math>n_2</math>, incluyéndolos a ambos. Un camino entre un nodo y sí mismo está formado únicamente por ese nodo. El algoritmo debe recorrer <b>como máximo una vez</b> cada nodo del árbol, que no necesariamente es completo. Se considerará incorrecto a un algoritmo que no cumpla con esta condición. | ||
[[File:Grafo_de_ejemplo_Ej3_Recu_2p_1C_2015_AyED2.jpg|600px]] | |||
<!-- Acá había un ejemplo de máxima suma, pero es una imagen, así que no la transcribí --> | <!-- Acá había un ejemplo de máxima suma, pero es una imagen, así que no la transcribí --> | ||
Se pide dar un algoritmo MáximaSumaCamino(a: ab(int)) -> int que resuelva el problema utilizando la técnica de Dividir y Conquistar, calculando y justificando claramente su complejidad. El algoritmo debe tener una complejidad temporal de peor caso igual o mejor que <math>O(n)</math> siendo <math>n</math> la cantidad de nodos del árbol. | Se pide dar un algoritmo MáximaSumaCamino(a: ab(int)) -> int que resuelva el problema utilizando la técnica de Dividir y Conquistar, calculando y justificando claramente su complejidad. El algoritmo debe tener una complejidad temporal de peor caso igual o mejor que <math>O(n)</math> siendo <math>n</math> la cantidad de nodos del árbol. | ||
Revisión del 19:15 19 sep 2017
17 de julio de 2015
Aclaraciones
- El parcial es a libro abierto
- Entregar cada ejercicio en hojas separadas
- Incluir en cada hoja el número de orden asignado, número de hoja, apellido y nombre.
- Al entregar el parcial, completar el resto de las columnas en la planilla.
- Cada ejercicio se calificará con MB, B, R o M, y podrá recuperarse independientemente de los demás. La cursada podrá aprobarse con hasta 1 (un) ejercicio R (regular) en cada parcial (post-recuperatorios), siempre y cuando ninguno de ellos sea un ejercicio 1. Para más detalles, ver "Información sobre la cursada" en el sitio Web.
Ejercicio 1: Diseño
Una importante empresa de software intenta insertarse en el mercado de los buscadores web. Para eso desean diseñar un motor de búsqueda, que inicialmente será muy rudimentario. En esta primera versión, el motor de búsqueda sólo podrá indexar documentos y realizar búsquedas por dos palabras clave.
Un documento no es más que una secuencia de palabras, y las palabras son cadenas de caracteres del alfabeto castellano (más los símbolos de puntuación usuales). En todo momento pueden indexarse nuevos documentos, que nunca de desindexan. Cada documento tiene, además, un nombre único que lo identifica que, eventualmente, podrá cambiarse. Los nombres de los documentos tienen una longitud no acotada. Lo mismo puede suceder con los documentos, que pueden tener cualquier cantidad de palabras, y estas palabras pueden ser de cualquier longitud.
Como en todo motor de búsqueda, el objetivo es encontrar documentos a partir de palabras clave. En esta versión sólo se podrán hacer búsquedas del tipo (Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle palabra_1 \land palabra_2} ) que devolverán el conjunto de documentos que contienen ambas palabras (tanto Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle palabra_1} como Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle palabra_2} ).
Por ejemplo, un documento que consiste en la secuencia de palabras "¡Qué genio tiene el ingenuo de Eugenio!" será parte del conjunto de respuestas para las búsquedas (genio Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \land} ingenuo) y (el Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \land} Eugenio!). Por el contrario, este documento no estará en el conjunto de respuestas si la búsqueda es (Eugenio! Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \land} ornitorrinco).
TAD Documento ES Secu(Palabra)
TAD Nombre ES String
TAD Palabra ES String
TAD Buscador
generadores:
iniciar: -> buscador
indexarDocumento: buscador b X nombre n X secu(palabra) d -> buscador {n !E documentos(b)}
cambiarNombre: buscador b X nombre n1 X nombre n2 -> buscador {n1 E documentos(b) ^ n2 !E documentos(b)}
observadores básicos:
documentos:buscador -> conj(nombre)
texto: buscador b X nombre n -> secu(palabra) {n E documentos(b)}
otras operaciones:
buscar: buscador b X palabra p1 X palabra p2 -> conj(nombre)
axiomas: ...
Fin TAD
Diseñe el TAD Buscador respetando los siguientes requerimientos de complejidad temporal en el peor caso:
- indexarDocumento(b, n, d)
Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O(long(n) + long(d) * max_p(d) * docs(b) * max_n(b))}
- buscar(b, p1, p2)
Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O(long(p_1) + long(p_2) + max_n(b) * docs(b))}
- texto(b, n)
Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O(long(n))}
donde Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle max_p(d)} es la longitud de la palabra más larga en Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle d} ; Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle max_n(b)} es la longitud del nombre del documento más largo en Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b} ; y Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle docs(b)} es la cantidad de documentos indexados por Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b} hasta el momento.
a) Muestre la estructura de representación propuesta. Explique para qué sirve cada parte de la estructura, o utilice nombres autoexplicativos.
b) Escriba el pseudocódigo del arlgoritmo buscar(in b: estr, in p1 : palabra, in p2 : palabra).
Justifique claramente cómo y por qué los algoritmos, la estructura y los tipos soporte permiten satisfacer los requerimientos pedidos. No es necesario diseñar los módulos soporte, pero sí describirlos, justificando por qué pueden (y cómo logran) exportar los órdenes de complejidad que su diseño supone.
Ejercicio 2: Ordenamiento
a) FIGFA (Federación Intergaláctica de Fútbol Asociado) maneja la información de miles de millones de equipos que participan en los distintos torneos de fútbol de todo el universo. Para cada equipo se calcula un puntaje que sirve para elaborar el ránking universal de equipos, que puede consultarse en su página web. FIGFA es muy desorganizada y no tiene optimizada esta información, es decir que arma el ránking desde cero cada vez que alguien lo consulta. Por otra parte, los registros históricos de la página web muestran que, en prácticamente todos los casos, a los visitantes sólo les interesa conocer los primeros 100 equipos del ránking. Sugoera a FIGFA dos algoritmos de sorting que considere apropiados para la generación del ránking, y uno que considere inapropiado. Justifique por qué en cada caso.
b1) La Real Academia Española mantiene un compendio completo del vocabulario español. Este compendio es simplemente la lista ordenada de todas las palabras del lenguaje. Al fina de cada año se enriquece el lenguaje con varias palabras nuevas. Esto se hace agregando al compendio del año anterior un conjunto desordenado de nuevas palabras. Obviamente, para obtener el nuevo compendio anual es necesario reordenarlo. Se estima que cada año se agrega una cantidad de palabras equivalente al 5% del tamaño completo del compendio del año anterior. Sugiera qué estrategias de ordenamiento son más apropiadas en esta situación. Justifique.
b2) El hecho de que se agregue un 5% de palabras nuevas, ¿Es relevante? ¿Cambiaría su respuesta (y cómo) su cada año se agregase un 50% de palabras nuevas? ¿Y si fuese un 100%, es decir se duplicara el vocabulario cada año?
Ejercicio 3: Dividir y conquistar
Dado un árbol binario de números enteros, se desea calcular la máxima suma de los nodos pertenecientes a un camino entre dos nodos cualesquiera del árbol. Un camino entre dos nodos Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n_1} y Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n_2} está formado por todos los nodos que hay que atravesar en el árbol para llegar desde Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n_1} hasta Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n_2} , incluyéndolos a ambos. Un camino entre un nodo y sí mismo está formado únicamente por ese nodo. El algoritmo debe recorrer como máximo una vez cada nodo del árbol, que no necesariamente es completo. Se considerará incorrecto a un algoritmo que no cumpla con esta condición.
Se pide dar un algoritmo MáximaSumaCamino(a: ab(int)) -> int que resuelva el problema utilizando la técnica de Dividir y Conquistar, calculando y justificando claramente su complejidad. El algoritmo debe tener una complejidad temporal de peor caso igual o mejor que Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O(n)} siendo Error al representar (SVG o PNG como alternativa (MathML puede ser habilitado mediante plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n} la cantidad de nodos del árbol.