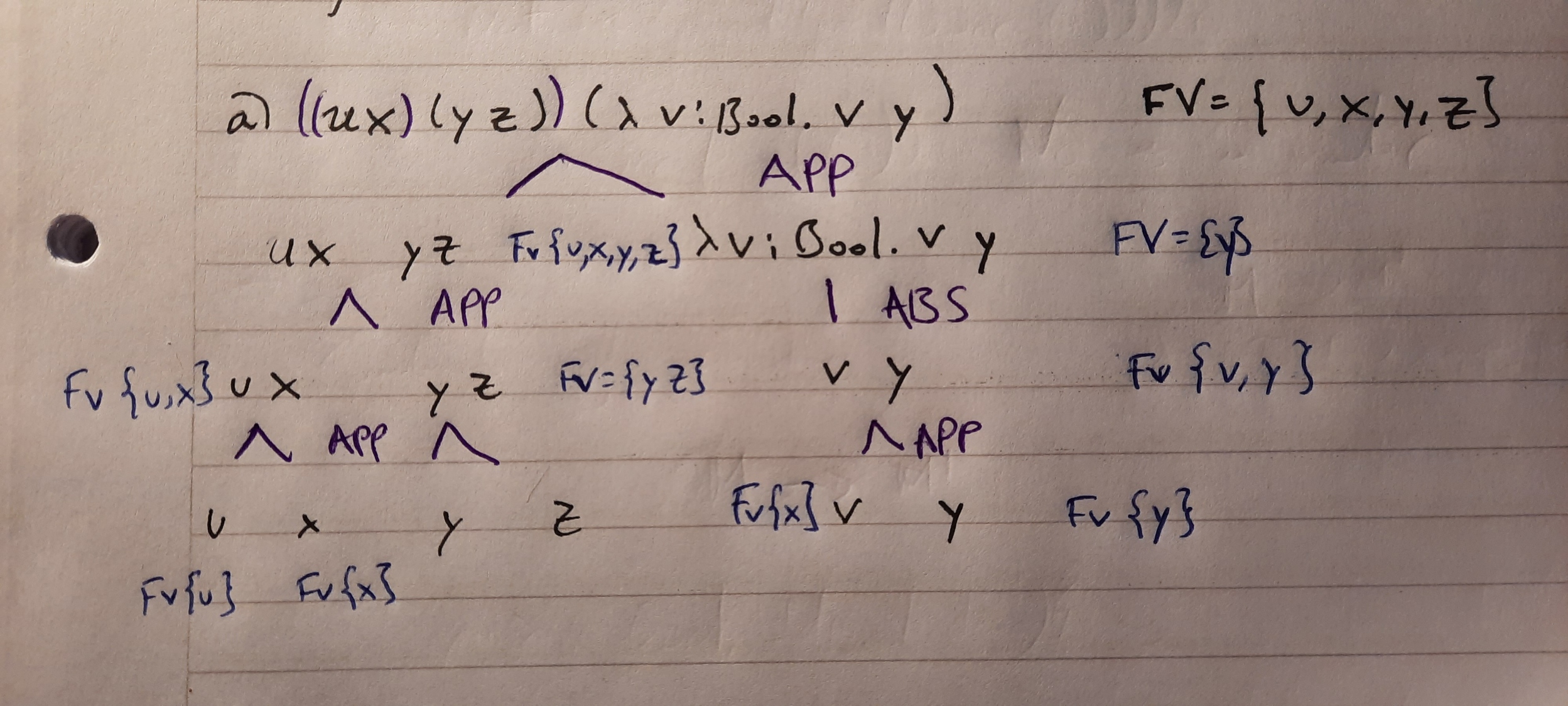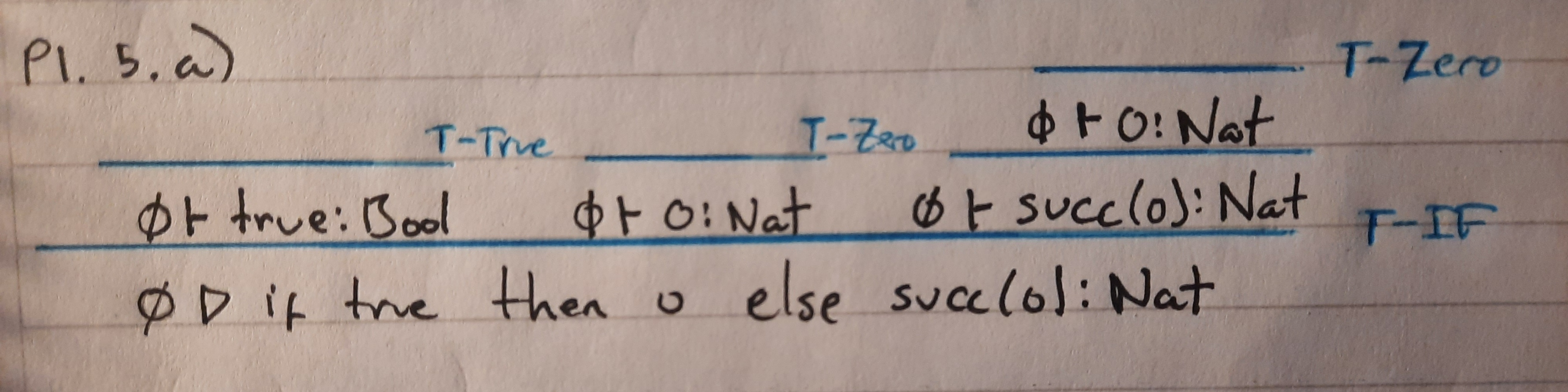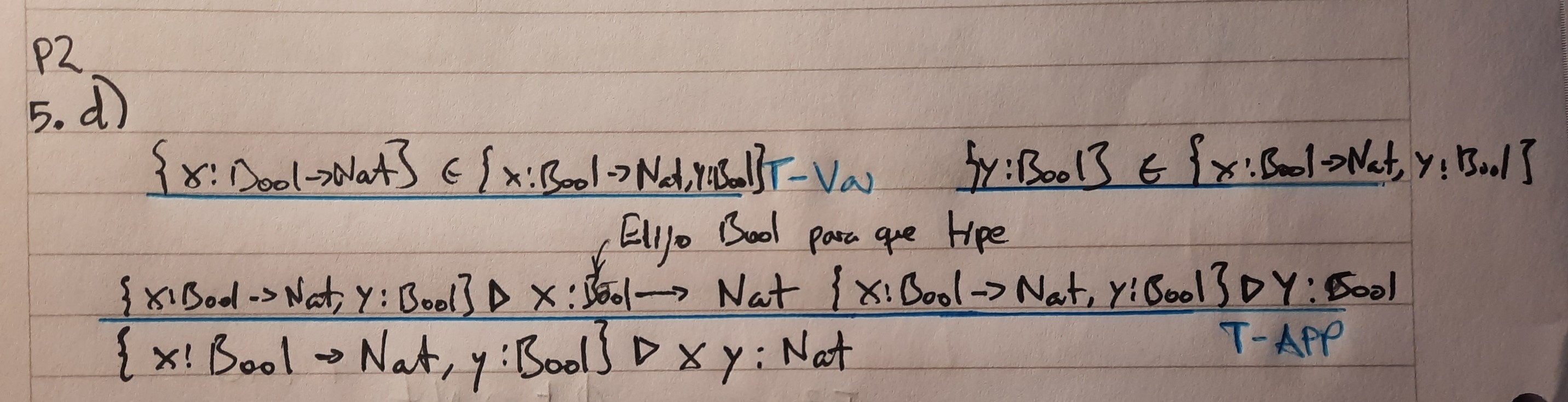Diferencia entre revisiones de «Práctica 2 (Paradigmas)»
Sin resumen de edición |
|||
| Línea 110: | Línea 110: | ||
a) ∅ . if true then 0 else succ(0) : Nat | a) ∅ . if true then 0 else succ(0) : Nat | ||
[[Archivo:5.a.jpg|none]] | |||
b) {x : Nat, y : Bool} . if true then false else (λz : Bool. z) true : Bool | b) {x : Nat, y : Bool} . if true then false else (λz : Bool. z) true : Bool | ||
[[Archivo:5b.jpg|none]] | |||
c) ∅ . if λx: Bool. x then 0 else succ(0) : Nat | c) ∅ . if λx: Bool. x then 0 else succ(0) : Nat | ||
Falta el resto del cuerpo del if ya que se agrupa de izq pero el lambda se come toda la expresión si no se le ponen parentesis. | Falta el resto del cuerpo del if ya que se agrupa de izq pero el lambda se come toda la expresión si no se le ponen parentesis. | ||
d) {x : Bool → Nat, y : Bool} . x y : Nat | d) {x : Bool → Nat, y : Bool} . x y : Nat | ||
[[Archivo:5d.jpg|none]] | |||
== Ejercicio 6 == | == Ejercicio 6 == | ||
Revisión del 20:30 6 oct 2021
SINTAXIS
Ejercicio 1
Determinar qué expresiones son sintácticamente válidas (es decir, pueden ser generadas con las gramáticas presentadas) y determinar a qué categoría pertenecen (expresiones de términos o expresiones de tipos):
a) x ---------VALIDO, expresiones de términos
b) x x ---------VALIDO, expresiones de términos
c) M --------- No es un término
d) M M --------- No es un término
e) true false ---------VALIDO, expresiones de términos
f) true succ(false true) ---------VALIDO, expresiones de términos
g) λx.isZero(x) --------- Falta tipo
h) λx: σ. succ(x) --------- Falta tipo, sigma no es un tipo valido
i) λx: Bool. succ(x) ---------VALIDO, expresiones de términos
j) λx: if true then Bool else Nat. x --------- Falta tipo
k) σ --------- Sigma no es un tipo valido
l) Bool ---------VALIDO, expresiones de tipos
m) Bool → Bool ---------VALIDO, expresiones de tipos
n) Bool → Bool → Nat ---------VALIDO, expresiones de tipos
ñ) (Bool → Bool) → Nat ---------VALIDO, expresiones de tipos
o) succ true --------- Si succ fuera una variables seria una aplicación, pero el enunciado dice que las variables se representan con una letra por lo cual a succ como termino le faltan los paréntesis.
p) λx: Bool. if 0 then true else 0 succ(true) ---------VALIDO, expresiones de términos
Ejercicio 2
Mostrar un término que utilice al menos una vez todas las reglas de generación de la gramática y exhibir su árbol sintáctico.
(λx: Bool. if isZero(succ(pred(x))) then true else false) x
app / \
(λx: Bool. if isZero(succ(pred(x))) then true else false) x
abs /
if isZero(succ(pred(x))) then true else false
ITF / | \
isZero(succ(pred(x)) true false
/
succ(pred(x))
/
pred(x)
/
x
Ejercicio 3
a) Marcar las ocurrencias del término x como subtérmino en λx: Nat. succ((λx: Nat. x) x).
Dos ocurrencias, en el lamda, y en la aplicación dentro den succ()
b) Ocurre x1 como subtérmino en λx1 : Nat. succ(x2)?
No, x1 es una variable ligada y no un subtermino.
c) Ocurre x (y z) como subtérmino en u x (y z)?
u x (y z) = ((u x) (y z) ) se agrupa a izq, por lo tanto no es subtermino en el árbol sintáctico.
Ejercicio 4
Para los siguientes términos:
a) u x (y z) (λv : Bool. v y)
( (u x) (y z) ) (λv : Bool. v y )
b) (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v w
( ( ( λx: (Bool -> Nat) -> Bool. λy: Bool ->Nat. λz : Bool. (x z) (y z) ) u) v ) w
c) w (λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u v
( ( w (λx : (Bool -> Nat) -> Bool. λy Bool -> Nat. λz: Bool. (x z) (y z) ) ) u) v
Se pide:
i Insertar todos los paréntesis de acuerdo a la convención usual.
c. Muy parecido al b pero queda una abstracción a la derecha.
ii Dibujar el árbol sintáctico de cada una de las expresiones.
iii Indicar en el árbol cuáles ocurrencias de variables aparecen ligadas y cuáles libres.
iv ¾En cuál de los términos anteriores ocurre la siguiente expresión como subtérmino?
(λx: Bool → Nat → Bool. λy : Bool → Nat. λz : Bool. x z (y z)) u
En el b
TIPADO
Ejercicio 5 (Derivaciones)
Demostrar o explicar por qué no puede demostrarse cada uno de los siguientes juicios de tipado.
a) ∅ . if true then 0 else succ(0) : Nat
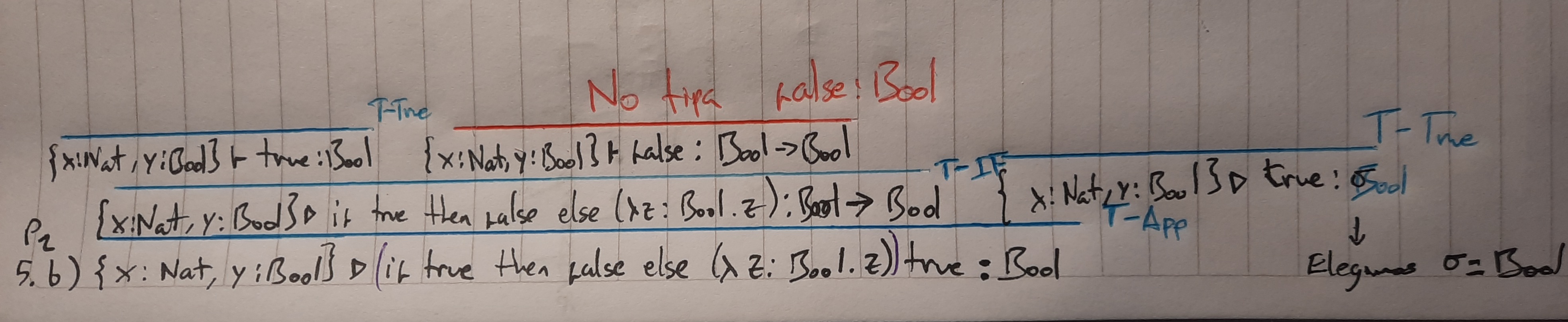
b) {x : Nat, y : Bool} . if true then false else (λz : Bool. z) true : Bool
c) ∅ . if λx: Bool. x then 0 else succ(0) : Nat
Falta el resto del cuerpo del if ya que se agrupa de izq pero el lambda se come toda la expresión si no se le ponen parentesis.
d) {x : Bool → Nat, y : Bool} . x y : Nat
Ejercicio 6
Determinar qué tipo representa σ en cada uno de los siguientes juicios de tipado.
a) ∅ . succ(0) : σ NAT
b) ∅ . isZero(succ(0)) : σ BOOL
c) ∅ . if (if true then false else false) then 0 else succ(0) : σ NAT
Ejercicio 7
Determinar qué tipos representan σ y τ en cada uno de los siguientes juicios de tipado. Si hay más de una solución, o si no hay ninguna, indicarlo.
a) {x: σ} . isZero(succ(x)) : τ ----- σ = Nat y τ = Bool
b) ∅ . (λx: σ. x)(λy : Bool. 0) : σ ----- σ = Bool -> Nat
c) {y : τ} . if (λx: σ. x) then y else succ(0) : σ ----- No tiene solución
d) {x: σ} . x y : τ ----- σ = No tiene solución
e) {x: σ, y : τ} . x y : τ ----- σ = CualquierCosa -> τ y τ=CualquierCosa
f) {x: σ} . x true : τ ------σ = Bool -> τ y τ=CualquierCosa
g) {x: σ} . x true : σ ----- σ = Bool -> CualquierCosa
h) {x: σ} . x x : τ ------ No tiene solución