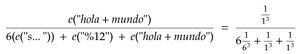IngSoft2 primer parcial 06/10/2022
Ejercicio 1
Sea el siguiente programa
def test_me(n: int) -> int; 1: r: int = 0 2: if n>=0: 3: i: int=0 4: while i < n: 5: if i%2 == 1: 6: r = r+i 7: i = i+1 8: return r
Usando el operador de mutación ROR (modifica una comparación aritmética reemplazandola por <,>,<=,>=,==,!=,false,true) exhibir tres mutantes tales que:
- Un mutante con un test que lo mata fuertemente (indicando la línea que cambió).
- Un mutante con un test que lo mata debilmente, pero no fuertemente (indicando la línea que cambió).
- Un mutante equivalente tal que no exista test que lo detecte ni débil ni fuertemente (indicando la línea que cambió).
Resolución
(Aclaración: pregunté a Juan Pablo y aclaró que valía dar un mutante para el que existieran tests que lo matan débil y fuertemente, mientras yo dé test que lo mata débilmente en el caso del inciso 2). 1. Un mutante en el que la línea 4 muta a "while i>n" es matado fuertemente por el test:
testA(): assertEquals(1, test_me(2))
ya que test_me mutada devolverá 0 en vez de 1.
2. Un mutante en el que la línea 4 cambia por "while i <=n" es matado débilmente por el test:
testB(): assertEquals(1, test_me(2))
ya que test_me mutada seguirá devolviendo 1 pero cambia el estado interno del programa, i llega a valer 3 en vez de quedar en 2.
3. Un mutante equivalente en el que la línea 5 muta a "if i%2 >=1" cumple lo pedido ya que la operación módulo 2 nunca devuelve más de 1, por lo que el comportamiento del programa nunca cambia.
Ejercicio 2
Sea el siguiente programa test_me del ejercicio #1.
- Escribir el árbol de cómputo del programa (con unroll de 1 del while, es decir en vez de while se lo toma como un if).
- Completar la siguiente tabla con la ejecución simbólica dinámica del programa de forma manual, indicando para cada iteración:
- El input concreto utilizado
- La condición de ruta (ie path condition) que se produce de ejecutar el input concreto, asumiendo que el valor simbólico inicial es n = n0.
- La fórmula lógica (no es necesario escribirla en SMTLib) que se envía al demostrador de teoremas de acuerdo al algoritmo de ejecución simbólica dinámica.
- El resultado posible que podría producir un demostración de teoremas (ej Z3).
| Iteración | Input Concreto | Condición de Ruta | Fórmula enviada al demostrador | Resultado posible |
|---|---|---|---|---|
| 1 | n=0 | ... | ... | ... |
| 2 | ... | ... | ... | ... |
| ... | ... | ... | ... | ... |
Resolución
1. Árbol de cómputo. Uso unroll de 1 (es decir "while i<n" cambia a "if 0<n").
Uso los renombres: C1: n0 >= 0 C2: 0 < n0 C3: 0%2 == 1
C1
/ \
T / \ F
C2 (it. 3)
/ \
T / \ F
C3 (it. 1)
/ \
T / \ F
UNSAT (it. 2)
2.
| Iteración | Input Concreto | Condición de Ruta | Fórmula enviada al demostrador | Resultado posible |
|---|---|---|---|---|
| 1 | n=0 | C1 ^ ¬C2 | n>=0 and 0<n | n0 = 1 |
| 2 | n=1 | C1 ^ C2 ^ ¬C3 | n>=0 and 0<n and 0%2==1 | UNSAT |
| n<0 | n0 = -1 | |||
| 3 | n=-1 | ¬C1 | END | END |
Ejercicio 3
Sea el programa test_me del ejercicio #1 y el siguiente test suite:
class TestSuite(unittest.TestCase):
def test_1(self):
self.assertEqual(0, test_me(-1000))
def test_2(self):
self.assertEqual(0, test_me(0))
def test_3(self):
self.assertEqual(0, test_me(1))
- ¿Cuál es el valor de distancia de branch no normalizada para cada decisión si ejecutamos el test suite? (Con k=1).
- ¿Cuál es el cubrimiento de líneas?
- ¿Cuál es el cubrimiento de branches?
Resolución
1. Las branch distances resultantes luego de ejecutar todo el test suite son (con k=1):
| C1 | C2 | C3 | |
|---|---|---|---|
| dist_true | 0 | 0 | 1 |
| dist_false | 0 | 0 | 0 |
2.
- test_1 cubre lineas 1,2,8
- test_2 cubre lineas 1,2,3,4,8
- test_3 cubre lineas 1,2,3,4,5,7,8
Por lo que la cobertura de la test suite es de 7/8 líneas.
3.
- test_1 cubre C1 por false
- test_2 cubre C1 true, C2 false
- test_3 cubre C1 true, C2 true y false, C3 false.
Por lo que la cobertura de la test suite es de 5/6 branches.
Ejercicio 4
Sea el siguiente programa cgi_decode:
def cgi_decode(s):
# Mapping of hex digits to their integer values
hex_values={
'0': 0 ,'1': 1,'2': 2 ,'3': 3 ,'4': 4 ,
'5': 5 ,'6': 6 ,'7': 7 ,'8': 8 ,'9': 9 ,
'a': 10 ,'b': 11 ,'c': 12 ,'d': 13 ,'e': 14 ,'f': 15 ,
'A': 10 ,'B': 11 ,'C': 12 ,'D': 13 ,'E': 14 ,'F': 15 ,
}
t = ""
i = 0
while i<len(s): #c1
c = s[i]
if c == '+': #c2
t +=' '
elif c == '%': #c3
digit_high, digit_low = s[i + 1], s[ i + 2 ]
i += 2
if digit_high in hex_values and digit_low in hex_values : #c4 y c5
v = hex_values[digit_high]*16 + hex_values[digit_low]
t += chr(v)
else:
raise ValueError("Invalid Encoding")
else:
t += c
i += 1
return t
Asumiendo que tenemos un boosted greybox fuzzer con exponente a=3. Sea el siguiente conjunto inicial de inputs: "si", "s2", "s3", "s4", "s5", "s6", "%12", "hola+mundo". ¿Cuál es la probabilidad que el fuzzer elija el input "hola+mundo" para mutar?
Resolución
"s1", "s2", ..., "s6" todas recorren el mismo camino, "%12" y "hola+mundo" recorren otros caminos. Por lo tanto como la energía de un input se calcula
e(s) = 1 / f(p(s))^a
Donde f(p(s)) es la frecuencia de apariciones del camino s y el exponente a es 3, la probabilidad de elegir "hola+mundo" será