Práctica 1: Transmisión de información (Teoría de las Comunicaciones)
Ejercicio 01
¿Qué cantidad de información se obtiene de la observación de los siguientes experimentos u objetos?
a. La tirada de una moneda equilibrada.
b. La tirada de un dado equilibrado.
c. Un codón (triplete de bases de ADN) en un genoma, donde cada base puede tomar 4 valores: A,T,C,G.
d. Una letra en un libro de Borges.
Rta:
Información de un evento: I(s) = -log2(P(s)) con P(s) la probabilidad del evento s
a. I(1/2) = -log2(1/2) = 1 bit
b. I(1/6) = -log2(1/6) = 2,58 bits
c. I( (1/4)^3 ) = -log2( (1/4)^3 ) = -log2(1/64) = 6 bits
d. I(#Cantidad Aparicion de letra "?"/ #Cantidad total de letras del libro)
Ejercicio 02
Una fuente de información binaria con memoria nula produce el símbolo s0 con probabilidad p0 y el símbolo s1 con probabilidad p1 = 1 - p0.
a. Formular la entropía de la fuente como función de p0.
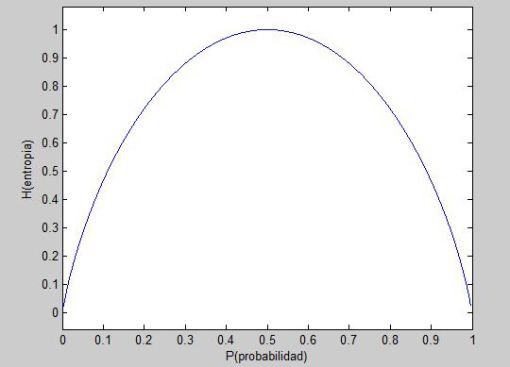
b. Graficar H(p0).
c. Dar una interpretación de los puntos de la gráfica que considere interesantes.
Rta:
Entropía de una fuente: H(S) = SUMATORIAseS P(s) I(s)
a. H(S) = p0 * I(s0) + (1 - p0) * I(s1) = p0 * -log2(p0) + (1 - p0) * -log2(1 - p0)
c. 0<=H<=log2 2
Ejercicio 03
Para la siguiente fuente
S = [P(A) = 0:4; P(B) = 0:3; P(C) = 0:2; P(D) = 0:1]
se proponen 3 códigos posibles
1. A = 00 ; B = 01 ; C = 11 ; D = 010
2. A = 0 ; B = 01 ; C = 011; D = 111
3. A = 1 ; B = 01 ; C = 001 ; D = 0001
a. ¿Cuáles son instantáneos?
b. ¿Cuáles son unívocamente decodificables?
c. ¿Cuál es más eficiente (H/L)?
d. ¿Alguno presenta pérdida de información?
Rta:
a. Un código es instantáneo o libre de prefijos si no codifica ningún símbolo como prefijo de otro.
1.No, B es prefijo de D.
2.No, A es prefijo de B.
3.Si, bit 1 sirve como limitador.
b. Un código es unívocamente decodificable si ninguna tira de símbolos del alfabeto código admite más de una única decodificación.
1.Si.
2.Si.
3.Si. Instantaneo --> Unívocamente decodificable.
c. Largo promedio de un código: L(C) = SUMATORIAseS P(s) l(C(s)) con l(C(s)) el largo de la codificación del símbolo s
L(C1) = P(A) * l(C(A)) + P(B) * l(C(B)) + P(C) * l(C(C)) + P(D) * l(C(D)) = 0.4 * 2 + 0.3 * 2 + 0.2 * 2 + 0.1 * 3 = 2.1
L(C2) = 1.9
L(C3) = 2
Dado que las probabilidades no cambian, la entropía de S es siempre igual (puntualmente, su valor es H(S) = 1,85). Luego, ofrecerá mejor rendimiento aquél código que minimice su longitud media. A simple vista queda claro que el código buscado es C2, cuya longitud media es L(C2) = 1,9.
d. Un código C sobre una fuente S codifica sin pérdida de información sii H(S) <= L(C)
Tenemos que H(S) < L(C2) < L(C3) < L(C1). Luego, ninguna de las tres longitudes medias es menor que la entropía de la fuente, lo cual garantiza que las tres codificaciones son sin pérdida de información.
Ejercicio 04
¿Cuánto vale la entropía y la longitud de la codificación de cada símbolo para las fuentes de información de los siguientes casos? Asumir que la codificación se da bajo el código óptimo.
a. 2 símbolos equiprobables
b. 4 símbolos equiprobables
c. 6 símbolos equiprobables
d. 8 símbolos equiprobables
e. 10 símbolos equiprobables
f. N símbolos equiprobables
Rta:
H(S) = SUMATORIA seS P(p0) * I(s0) = #S * (1/#S) * -log2(1/#S) = log2(#S)
C es óptimo sii L(C) es mínima (i.e., todo otro código sobre S tiene mayor o igual longitud promedio). --> H(S) = L(C). Siempre que H(S) sea potencia de 2, sino el próximo valor entero.
a. H(S) = L(C) = log2(2) = 1
b. H(S) = L(C) = log2(4) = 2
c. H(S) = log2(6) L(C) = [log2(6)] = 3
d. H(S) = L(C) = log2(8) = 3
e. H(S) = log2(10) L(C) = [log2(10)] = 4
f. H(S) = log2(N) L(C) = [log2(N)]
Ejercicio 05
Considere una señal de video en escala de grises que transmite imágenes a una resolución 640 x 480 píxeles, de los cuales cada uno puede asumir 10 niveles diferentes de brillo. Supongamos que la tasa de transmisión es de 30 imágenes por segundo y que la relación señal a ruido es de 30 dB.
a. Calcular la entropía de la fuente si todas las imágenes fueran equiprobables.
b. ¿Cuántos bits son necesarios para codificar cada imagen de manera óptima e instantánea con un código que asigne el mismo largo a todas las imágenes?
c. Calcular el ancho de banda mínimo requerido para soportar la transmisión de la señal resultante.
Rta:
a.log2(#S) (fuente equiprobables), Donde #S = 10^(640 x 480), entonces log2(10^(640 x 480)) = (640 x 480) * log2(10) = 1,02049631 × 10^6
b. En esta fuente equiprobable, tenemos que H(S) = log2(n), no siendo n una potencia de 2. Esto implica que no podemos pensar en recurrir a un código (óptimo) que asigne log2(n) bits por imagen, pues por supuesto estos valores deben ser números enteros. No obstante, la aproximación más cercana a este valor es tomar exactamente [log2(n)](próximo número entero) bits por imagen. De esta forma podremos armar un código que sea instantáneo (cada imagen recibe una tira de bits distinta) y “localmente óptimo”, entendiendo por esto que todo otro código que mapee cada imagen a una tira de bits de igual largo debe necesariamente poseer una longitud media igual o mayor.
L(C) = 1020497
c.
Teorema de Shannon: C[bps] = B[Hz] * log2(1 + SNR[veces]) con SNR[veces] = 10SNR[dB]=10 y B el ancho de banda disponible. Velocidad de transmisión sin pérdida de información: Vtx[bps] <= C[bps], con V max tx = C
Para responder este ítem, hay que usar el teorema de Shannon: C = B * log2(1 + SNR). Primero, la relación señal-ruido hay que pasarla de decibeles a veces: SNR = 1030/10 = 1000. Luego, como se necesitan 30 imágenes por segundo, la capacidad de canal debe ser mayor o igual que L(C) * 30 bps. Entonces, B = 60 / log2(1001) = 6.02 Hz.
Vtx[bps] = 30 (imagenes x segundo) * 2 (L(C)) = 60 bps
Vtx[bps] <= C[bps]
B[Hz] = 60/log2(1+ 10^(30db/10)) = 6.02
Ejercicio 06
Calcule la Capacidad de Volumen (cantidad de bits que entran simultáneamente) en cada uno de los siguientes medios físicos de transmisión, asumiendo que se los utiliza a su máxima Capacidad de Transmisión (es decir, sin pérdida de información):
a. D = 100km, Vprop = 200000km/s, SNR = 100dB, B = 400Hz
b. D = 100km, Vprop = 200000km/s, SNR = 10dB, B = 400kHz
c. D = 100km, Vprop = 300000km/s, SNR = 10dB, B = 400kHz
d. D = 100m, Vprop = 300000km/s, SNR = 10dB, B = 400kHz
Rta:
Capacidad de Volumen de un canal (también "Producto Delay por Velocidad de Transimisión" o "Producto Delay por Ancho de Banda"): Cvol[bits] = Delay * Vtx
Delay: Delay[Seg] = Ttx + Tprop
Tiempo de Transmisión de un bit: Ttx[Seg] = 1/Vtx
Velocidad de transmisión sin pérdida de información: Vtx[bps] <= C[bps] -> Vtx max [bps] = C[bps]
Capacidad de un canal (limitado en potencia, en acho de banda y con ruido): C[bps] = B[Hz] * log2(1 + SNR[Veces]) con SNR[veces] = 10^(SNR[dB]/10) y B el ancho de banda disponible.
Tiempo de Propagación de un bit: Tprop[Seg] = D/V con D la distancia del enlace y V la velocidad de propagación de la forma de onda en el medio físico.
Cvol[bits] = ( 1/C[bps] + D/V ) * C[bps] = 1 + (D*C[bps])/Vprop
a.
C[bps] = 400Hz * log2(1 + 10^(100dB/10) = 13288 bps
D = 100km
V = Vprop = 200000km/s
Cvol[bits] = 1 + (13288 bps * 100Km)/200000km/s = 7 bits
b.
C[bps] = 400KHz * log2(1 + 10^(10dB/10) = 1383 kbps = 1383000 bps
D = 100km
V = Vprop = 200000km/s
Cvol[bits] = 1 + (100km*1383000 bps)/200000km/s = 692 bits
c.
C[bps] = 400KHz * log2(1 + 10^(10dB/10) = 1383 kbps = 1383000 bps
D = 100km
V = Vprop = 300000km/s
Cvol[bits] = 1 + (100km*1383000 bps)/300000km/s = 462 bits
d.
D = 100m = 0.1km
V = Vprop = 300000km/s
Cvol[bits] = 1 + (0.1km*1383000 bps)/300000km/s = 1 bit
Ejercicio 07
Un satélite orbita la tierra tomando muestras meteorológicas. Se desea establecer un enlace entre dicho satélite y una base central en la superficie terrestre. Dicho medio de transmisión soporta una velocidad de transmisión de 100 Mbps. Si la información viaja a una velocidad de propagación de 300000 km/s, ¿es posible que haya una distancia para la que el tiempo total de enviar 30Mb sea menor que 0.04 segundos?
Rta:
Vtx: 100 Mbps
Vprop: 300000 km/s
El delay representa el tiempo total que tardamos en enviar información de un punto a otro: Delay = Ttx + Tprop
Ttx: tiempo de transmisión: Ttx = |datos|/Vtx
Tprop: tiempo de propagación: Tprop = D/Vprop
Ttx[Seg] = 30Mb/100Mbps = 0.3 Seg
Delay[Seg] = 0.3 + (D/300000 km/s) <= 0.04 Seg -> (D/300000 km/s) <= -0.26 Seg -> D <= -78000 Km -> Por lo tanto, No es posible enviar en 30 Mb en menos de 0.04 Segundos.
Ejercicio 08
Suponga que se instala un enlace punto a punto de 100 Mbps entre la Tierra y una base en la Luna. La distancia entre la Luna y la Tierra es de aproximadamente 385000 km, y la velocidad de propagación de los datos es la velocidad de la luz (300000 km/s).
a. ¿Cuál es el Delay de ida de un bit? ¿Y el RTT de un bit del enlace?
b. ¿Cuántos bits entran simultáneamente en el canal?
c. Una cámara en la base lunar toma fotografías de la Tierra y las guarda en formato digital en un disco. Suponga que el Control de Misión en la Tierra desea descargar la última imagen que es de 25 Mb. ¿Cuál es el tiempo mínimo que puede transcurrir entre el momento en que se inicia el pedido del dato y finaliza la recepción? (Asumir que el mensaje de pedido es de 2Kb)
Rta:
Vtx: 100 Mbps = 100000000 bps
D: 385000 km
Vprop: 300000 km/s
a. Delay[Seg] = 1/100000000 bps + 385000 km/300000 km/s = 1.28 Seg
RTT = 2 * Delay = 2 * 1.28 Seg = 2.56 Seg.
b.
Cvol[bits] = Delay * Vtx = 1.28 Seg * 100 Mbps = 128 Mbits
c.
Mensaje de pedido es de 2Kb = 0,002 Mb
Descarga de datos es de 25 Mb
Enviar el pedido: Delay = 0,002Mb/100Mbs + 385000 km/300000 km/s = 1.28 Seg
Descarga de datos: Delay = 25Mb/100Mbs + 385000 km/300000 km/s = 1.53 Seg
Tiempo mínimo que puede transcurrir entre el momento en que se inicia el pedido del dato y finaliza la recepción: 1.28 Seg + 1.53 Seg = 2.81 Seg
Ejercicio 09
Un robot helicóptero transmite la señal de su cámara de video sobre un enlace inalámbrico que tiene una relación señal a ruido del orden de los 30dB, con un ancho de banda útil de 50kHz. Modelando la cámara como una fuente de información se obtiene que su entropía es de 5Kb. Asumiendo que se desea transmitir sin pérdida de información:
a. ¿Hasta cuántas imágenes por segundo es posible enviar?
b. Calcule el delay promedio de una imagen enviada por el robot a 2km de distancia (Vprop = 300000 km/s).
Rta:
a.
Vtx max = C[Kbps] = 50KHz * log2(1+10^(30db/10)) = 498,36 Kbps
Ttx = |DATOS|/Vtx = 1 Seg --> |DATOS| = Vtx = 498,36 kbps
H(S) <= L(C) = 5Kb --> |DATOS|/L(C) = 498.36Kb/5Kb = 99 Imagenes
b.
Delay[Seg] = Ttx + Tprop = 5Kb/498,36Kbps + 2km/300000km/s = 0.01004 Seg
Ejercicio 10
En el esquema de la figura hay 3 servidores haciendo broadcasting de video a través de un satélite. Cada servidor envía video sin comprimir con una resolución de 4Mb por imagen y 25 imágenes por segundo. Cada servidor está conectado al switch que se conecta a un satélite mediante un enlace satelital. El enlace satelital tiene una relación señal-ruido de 30dB.
servidor1 \
servidor2 - Switch - Satelite
servidor3 /
a. ¿Cuánto ancho de banda (Hz) será necesario en el enlace satelital para satisfacer el broadcasting de todos los servidores sin pérdida de información?
b. Si se modelaran las señales de los servidores como fuentes de memoria nula y la entropía de cada fuente fuera como se indica en la tabla, ¿qué señal se podría comprimir más? Explique.
Servidor1 Entropía 100
Servidor2 Entropía 180
Servidor3 Entropía 150
Rta:
a.
Vtx (Servidores) = 4Mb (resolucion) * 25 (Imagenes) * 3 (Servidores) = 300 Mbps
Sin perdida de información -> Vtx = C
Remplazo en Shannon -> B[MHz] = C[Mbps]/log2(1+SNR) = 300 Mbps/log2(1+10^3) = 30.12 MHz
b.
La codificación es sin pérdida de informacion si se cumple:
H(S) <= L(C(S))
Ejercicio 11
Un ciclista recorre un circuito montañoso con una cámara de video en su casco. Esta cámara transmite la señal capturada por un enlace inalámbrico cuya relación señal-a-ruido es de 20 dB, siendo además su ancho de banda útil 60 kHz. La cámara, por otro lado, puede modelarse como una fuente de información S en la que cada símbolo es cada una de las imágenes transmitidas.
a. Encontrar una cota superior para la cantidad media de imágenes que la cámara podrá enviar por segundo por el enlace, expresada en términos de H(S).
b. Supongamos un código C sobre S que asigna n bits al símbolo más probable de S y m bits al símbolo menos probable, siendo n > m. ¿Puede ser C un ¢odigo óptimo? Asumir que S no es equiprobable.
Rta: