Segundo parcial 24/11/2022 (IngSoft2)
Ejercicio 1
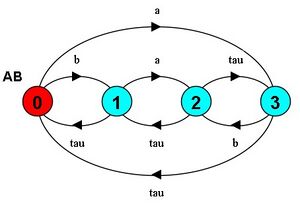
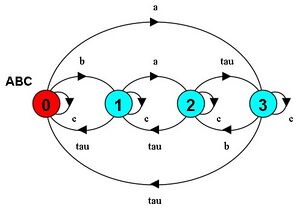
a) Dibuje los LTS para AB y ABC
A = (a -> c -> A).
B = (b -> d -> B).
||AB = (A||B)\{c,d}.
C = (c -> C).
||ABC = (AB || C).
Resolución
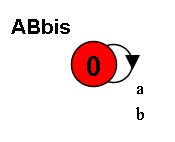
b) Proponga un LTS que sea débilmente equivalente a AB pero con menos estados. Demuestre que son equivalentes
Resolución
Para demostrar que son débilmente bisimilaresbasta con dar la relación de bisimilitud: [(0,0), (1,0), (2,0), (3,0)].
(Puede ser difícil ver por qué valen (1,0), (2,0) y (3,0), dejo la justificación de (1,0) a partir de la definición formal, las otras dos son análogas:
Sea Q el LTS de un nodo, 0ab el estado 0 del LTS AB y 0q el estado 0 de Q: - 1ab -a-> 2ab y 0q =a=> 0q y (2,0) esta en la relacion - 0q -b-> 0q y 1ab =b=> 1ab (porque 1 -tau-> 0 -b-> 1) y (1,0) esta en la relacion - 0q -a-> 0q y 1ab =a=> 2ab y (2,0) esta en la relacion
)
Ejercicio 2
En el siguiente ejemplo, el proceso TWOCOIN satisface la propiedad de profreso TAILS? Explique.
TWOCOIN = (pick ->COIN | pick ->TRICK).
TRICK = (toss -> heads -> TRICK |
toss -> heads -> TWOCOIN).
COIN = (toss -> heads -> COIN |
toss -> tails -> COIN).
progress TAILS = {tails}.
Resolución
La única forma de que TAILS nunca se cumpla es que siempre que estemos en el estado TWOCOIN se elija el camino a TRICK o elijamos la moneda TRICK una vez y de ahí siempre hagamos toss con esa misma moneda. Pero bajo fair choice, sabemos que cuando un estado es visitado infinitas veces, todas sus transiciones salientes también lo son. En las situaciones que mencioné antes, estaríamos visitando TWOCOIN y/o TRICK infinitas veces, por lo que eventualmente se seleccionará la moneda justa (COIN, que contiene tails) y se usará de ahí en más, cumpliendo la propiedad TAILS.
Ejercicio 3
Una solución clásica al problema de deadlock de los filósofos es que cada filósofo pueda hacer un timeout y devolver su palillo si no consigue su segundo palillo. Modifique el FSP dado a continuación para modelar esta solución clásica.
FORK = (get -> put -> FORK).
PHIL = (sitdown->left.get->right.get
->eat->left.put->right.put
->arise->PHIL).
||DINERS(N=5)=
forall [i:0..N-1]
(phil[i]:PHIL ||
{phil[i].left,phil[((i-1)+N)%N].right}::FORK
).
Resolución
const T=10.
TIMER = (right.get->TIMER[N]),
TIMER[0] = (timeout->TIMER),
TIMER[i:1..N]=(left.get->TIMER | tick->TIMER[i-1])\{tick}.
PHIL = (sitdown->right.get->WAIT),
WAIT = (timeout->right.put->arise->PHIL
| left.get->eat->left.put->right.put->arise->PHIL).
FORK = (get -> put -> FORK).
const N = 5.
||DINERS=
forall [i:0..N-1](
phil[i]:PHIL
|| phil[i]:TIMER
|| {phil[i].left,phil[((i-1)+N)%N].right}::FORK
).
Ejercicio 4: Verdadero o Falso? Justifique
a) p W q es una propiedad de safety y no es una propiedad de liveness. (Recuerde que Φ W Ψ se define como (Φ U Ψ) || []Φ)
Resolución
El ejercicio 4 lo hicimos regular o mal todos los que entregamos menos alguien que no conozco, así que no tengo la resolución chequeada. Confirmé con Uchitel que es verdadero (la propiedad es de safety y no de liveness), pero se esperaba que demostraramos utilizando las definiciones de que los contraejemplos de las propiedades de safety son trazas finitas/trazas infinitas para las propiedades de liveness. Si alguien lo hizo bien por favor agregue la resolución.
b) ([]p) U q es equivalente a [](p U q)
(Este lo hablé con Uchitel y me dijo que era correcto resolver así, pero no fue como lo hice en el parcial así que no lo tengo confirmado con corrección) La traza p, {p, q}, {p, ¬q}, {p, ¬q}, {p, ¬q}, .... cumple la primer propiedad pero no la segunda, porque la segunda habla de que siempre cuando vale p eventualmente valdrá q, en cambio la primera solo pide que si valió []p en algún momento, valga q una vez después.
Ejercicio 5
Escriba una estructura de kripke que satisfaga la fórmula AG EX p y no satisfaga la fórmula AG AX p
1) AG EX p: "Para todo camino, siempre vale que existe un camino donde en el próximo estado vale p" 2) AG AX p: "Para todo camino, siempre vale que en todo camino en el próximo estado vale p"
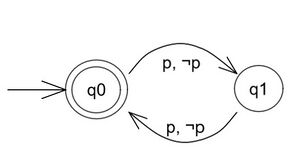
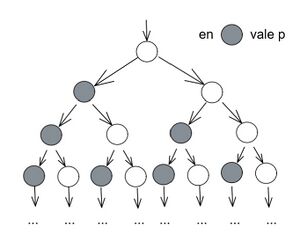
Una estructura de Kripke que satisfaga 1) pero no 2) sería
El árbol de cómputo es:
Siempre hay un próximo estado donde vale p, pero no en todos los próximos estados vale p.
Ejercicio 6
Escriba un büchi no generalizado que capture la propiedad [](p=>Xq)
Mientras no ocurra p vale, pero si ocurre p en el siguiente momento debe volver q.